くらげnote

"ぼやき" by くらげ(fal)

Windows 11 + WSL2 + Dockerで構築する安全なAIエージェント開発環境

技術系の何か

本記事では、Windows内の特定ディレクトリのみをAIエージェントに参照させ、それ以外のシステムや個人データから隔離した開発環境をゼロから構築する。 特定のツールに依存しない汎用的な構成とするが、本記事では例として「Antigravity IDE」を動かす環境を構築する。

全体構成

構成の概要は以下の通りである。

[ Windows 11 (ホスト) ]
  ├── C:\Users\... (完全遮断・アクセス不可)
  ├── C:\Users\<Windowsユーザー>\AI-shared (マウントする共有フォルダ)
        │
[ WSL2 (Ubuntu) ] ── (automount=false / Dockerホスト)
  └── Antigravity IDE (GUI)
        └── [ Docker コンテナ ]
              ├── AIエージェントの作業領域 (/workspace)
              ├── 参照フォルダ (/shared)
              └── コマンド実行・自動化プロセスの完全隔離

Step 1. [Windows] WSL2（Ubuntu）のセットアップ

まずはWSL2とデフォルトディストリビューションであるUbuntuを導入する。

1. WSL2のインストール

PowerShellを管理者として起動し、Linux用Windowsサブシステム（WSL）およびUbuntuディストリビューション(デフォルト)をインストールする。

wsl --install

# ダウンロード中: Linux 用 Windows サブシステム 2.7.11
# インストール中: Linux 用 Windows サブシステム 2.7.11
# Linux 用 Windows サブシステム 2.7.11 はインストールされました。
# この操作を正しく終了しました。
# ダウンロードしています: Ubuntu
# インストールしています: Ubuntu
# ディストリビューションが正常にインストールされました。'wsl.exe -d Ubuntu' を使用して起動できます
# Ubuntu を起動しています...
# Provisioning the new WSL instance Ubuntu
# This might take a while...
# Create a default Unix user account:

コマンド実行後、画面の指示に従い、システムの再起動を求められた場合は再起動を行う。 環境によっては、一度の実行でUbuntuまでインストールされず、再起動後に再度 wsl --install を実行する必要がある場合がある。

2. Windows側でのWSL network設定

Windowsホスト側の C:\Users\<ユーザー名>\.wslconfig ファイルを新規作成（または編集）し、以下の設定を記述して保存する。これによりネットワークの接続方式を設定する。

[wsl2]
networkingMode=NAT
dnsTunneling=true
autoProxy=true

Step 2. [WSL(Ubuntu)] WSL設定とディレクトリのマウント

WSL2内の設定を変更し、WindowsのCドライブ全体が自動的にマウントされないようにする。

[!TIP] マウント制限による Windows 側コマンド（Interop）の安全性確保 本環境では、WSL2からWindowsホストへの実行パス（Interop）自体は有効であるものの、Cドライブ全体のマウントを無効化（automount = false）している。 これにより、WSL2側からは powershell.exe や cmd.exe などのパスが見えず、実質的にマウントしたGoogle Chrome以外のホストコマンドは実行できない「ホワイトリスト状態」が作られ、安全性が向上する。

※ただし、万が一コンテナからWSL2（Ubuntu）へエスケープされ、さらにUbuntu側で管理者権限（sudo）を奪取された場合、攻撃者が手動でCドライブを強制マウントする可能性がある。 そのため、WSL2側では sudo 実行時に必ずパスワードを要求する設定（デフォルト状態）を維持するべきである。

1. パッケージの更新

sudo apt update
sudo apt upgrade

2. 自動マウントの制限設定

WSL（Ubuntu）のターミナルを起動し、設定ファイル /etc/wsl.conf をテキストエディタで開く。

sudo nano /etc/wsl.conf

以下の設定を /etc/wsl.conf に追記して保存する。 enabled = false により、Windowsのドライブ全体の自動マウントを無効化する。

[automount]
enabled = false
mountFsTab = true
options = "metadata,uid=1000,gid=1000,umask=022,fmode=11,dmode=755"

[interop]
appendWindowsPath = false # Windows側の環境変数を展開しない

[network]
generateResolvConf = false

3. DNSサーバーの設定とパッケージ更新

DNS名前解決を固定するためのDNSサーバー情報を書き込む。

# パブリックDNSを上書き
sudo rm -f /etc/resolv.conf
sudo bash -c 'cat << EOF > /etc/resolv.conf
nameserver 8.8.8.8
nameserver 1.1.1.1
EOF'

4. 特定フォルダおよびChromeのマウント設定

AIに共有するフォルダ（ここでは例として AI-shared）と、OAuth認証で使用するWindows側のGoogle Chromeのみをマウントする設定を行う。 マウント先となるディレクトリを作成し、ファイル /etc/fstab を開く。

# Windowsユーザー名を確認し、マウント先ディレクトリを作成
sudo mkdir -p /mnt/c/Users/<Windowsユーザ>/AI-shared
sudo mkdir -p /mnt/win-chrome

sudo nano /etc/fstab

/etc/fstab に以下の設定を追記し、特定のフォルダのみをマウントさせる。

C:/Users/<Windows側のユーザー名>/AI-shared /mnt/c/Users/<Windows側のユーザー名>/AI-shared drvfs metadata,noatime,gid=1000,uid=1000,defaults 0 0
C:/Program\040Files/Google/Chrome/Application /mnt/win-chrome drvfs defaults,uid=1000,gid=1000,umask=022 0 0

※マウントオプションで使用するユーザーID（uid）とグループID（gid）は、以下のコマンドで確認できる。初期登録ユーザーは通常どちらも 1000 である。

$ id <WSLのユーザー名>

5. WSLの再起動とマウント状態の確認

一度WSLをシャットダウンして設定を反映させ、目的のディレクトリのみが適切に見えているか確認する。 WindowsのPowerShellで以下のコマンドを実行する。

wsl --shutdown

# マウント状態と権限の確認
ls -ld /mnt/c/Users/<Windowsユーザ>/*
# 出力にAI-shared のみが表示され、他の個人フォルダが見えなければ成功

Step 3. [WSL(Ubuntu)] Docker Engineの導入（WSL2内）

Docker Desktopを経由せず、WSL2（Ubuntu）内に直接 Docker Engine を導入してコンテナ実行環境を準備する。

1. Dockerのインストール

Docker本体およびビルド用の拡張パッケージをインストールする。

# Docker のインストール（WSL2 Ubuntu内）
sudo apt install -y docker.io docker-compose-v2
sudo usermod -aG docker $USER
sudo apt update
sudo apt install -y docker-buildx

※インストール完了後、設定を反映させるために一度ターミナルを開き直す。 その後、docker run hello-world を実行し、sudoなしでコンテナが起動することを確認する。

2. Dockerデーモンの設定

DockerコンテナがWSL2のネットワーク構成に悪影響を与えないように設定を調整する。 /etc/docker/daemon.json を作成・編集する。

sudo mkdir -p /etc/docker
sudo bash -c 'cat << "EOF" > /etc/docker/daemon.json
{
  "dns": ["8.8.8.8", "1.1.1.1"],
  "max-concurrent-downloads": 1,
  "iptables": true
}
EOF'

Step 4. [WSL(Ubuntu)] Antigravity IDEインストール

AIエージェントの開発環境として利用する「Antigravity IDE」をWSL2内にインストールする。

1. 必要パッケージの導入とダウンロード・展開

依存ライブラリをインストールし、一時ディレクトリにダウンロードしたパッケージを展開して /opt 領域に配置する。 その後、パスの通った場所にシンボリックリンクを作成する。

# パッケージ
sudo apt install -y libgtk-3-0 libnss3 libasound2t64 xdg-utils

# 一時ディレクトリへ移動
cd /tmp

# 公式サイトから Linux版 (x64) アーカイブ (tar.gz)をダウンロード。URLは最新のものに書き換える
curl -fSL -o antigravity-ide.tar.gz "https://edgedl.me.gvt1.com/edgedl/release2/j0qc3/antigravity/stable/2.5.5-4923483625488384/linux-x64/Antigravity%20IDE.tar.gz"

# システム領域（/opt/antigravity）へ展開
sudo mkdir -p /opt/antigravity-ide
sudo tar -xzf antigravity-ide.tar.gz -C /opt/antigravity-ide --strip-components=1

# コマンド一発で起動できるようにシンボリックリンクを作成
sudo ln -sf /opt/antigravity-ide/antigravity-ide /usr/local/bin/antigravity-ide

2. Windowsブラウザ（Chrome）によるOAuth認証連携の設定

WSL2上のアプリケーションから呼び出されるWebブラウザを、Windows側のGoogle Chromeに転送するためのラッパースクリプトとデスクトップエントリを作成し、規定のブラウザとして登録する。

# 呼び出しスクリプトを作成
mkdir -p ~/.local/bin
cat << 'EOF' > ~/.local/bin/win-chrome-wrapper
#!/bin/bash
if [ -n "$1" ]; then
    /mnt/win-chrome/chrome.exe "$1" &
fi
EOF
chmod +x ~/.local/bin/win-chrome-wrapper

# ラッパースクリプト作成
mkdir -p ~/.local/bin ~/.local/share/applications
cat << 'EOF' > ~/.local/bin/win-chrome
#!/bin/bash
if [ -n "$1" ]; then
    /mnt/win-chrome/chrome.exe "$1" &
fi
EOF
chmod +x ~/.local/bin/win-chrome

# デスクトップエントリ作成
cat << 'EOF' > ~/.local/share/applications/win-chrome.desktop
[Desktop Entry]
Version=1.0
Name=Windows Chrome
Exec=/home/<Ubuntuユーザ>/.local/bin/win-chrome %u
Terminal=false
Type=Application
MimeType=text/html;text/xml;application/xhtml_xml;x-scheme-handler/http;x-scheme-handler/https;
EOF

# XDG既定ハンドラに設定
xdg-mime default win-chrome.desktop x-scheme-handler/http
xdg-mime default win-chrome.desktop x-scheme-handler/https
xdg-settings set default-web-browser win-chrome.desktop

3. 起動確認とライセンス認証

以下のコマンドを実行し、WSLg（GUI表示機能）を介してAntigravity IDEが立ち上がることを確認する。 起動後、指示に従いブラウザ経由でライセンスなどの認証を行う。

antigravity-ide

Step 5. [WSL(Ubuntu)] プロジェクト作成と docker-compose.yml の配置

AIエージェントを閉じ込めて実行する「サンドボックスコンテナ」を作成し、起動する。

1. プロジェクトディレクトリの作成

任意の場所にプロジェクト用のフォルダを作成して移動する。

mkdir -p ~/workspace/my-first-app/
cd ~/workspace/my-first-app

2. サンドボックス構成ファイルの作成

コンテナの定義ファイル docker-compose.yml を作成する。 Windows側の共有フォルダのみを、コンテナ内部へ読み取り専用（:ro）でマウントするように制限する。

services:
  agent-sandbox:
    container_name: agent-sandbox
    image: mcr.microsoft.com/devcontainers/base:ubuntu
    working_dir: /workspace
    environment:
      - HOME=/workspace
    volumes:
      - .:/workspace
      - /mnt/c/Users/<Windowsユーザ>/AI-shared:/shared:ro
    command: sleep infinity

workspaceフォルダはAIエージェントが読み書き可能であるため、機密情報は決して置かないように運用する。

3. コンテナの起動

バックグラウンドでサンドボックスコンテナを起動する。

sudo docker compose up -d

Step 6. [WSL(Ubuntu)] Antigravity IDEからコンテナへのアタッチと確認

1. コンテナへのアタッチ

  1. Antigravity IDE を起動する。 bash antigravity .
  2. エディタ上で Ctrl + Shift + P キーを押し、コマンドパレットを開く。
  3. Dev Containers: Attach to Running Container...（実行中のコンテナにアタッチ）を選択する。
  4. リストから agent-sandbox を選択し、コンテナ内に入る。

2. サンドボックス環境の隔離検証

アタッチしたコンテナの統合ターミナルで以下のコマンドを実行し、ファイルシステムが適切に制限されているかを確認する。

  • カレントディレクトリの確認: pwd を実行し、出力結果が /workspace になっていることを確認する。
  • 共有フォルダの確認: ls /shared を実行し、Windows側の AI-shared の中身のみが参照可能であることを確認する。
  • 隔離状態の確認: ls /mnt/c や ls /home を実行し、WindowsホストやWSL2側のシステム・個人データ領域に一切アクセスできないことを確認する。

定型文を送るLINE Botの作成

技術系の何か

やりたいこと

LINEの特定のグループトーク(あるいは特定の個人)に, 定型文を送る.

目次

前提条件

  • LINE公式アカウントは持っているものとします.
  • GAS(Google Apps Script)が使える環境

流れ

  1. 送るべきリクエストの簡単な説明
  2. チャンネルアクセストークンの取得
  3. グループID取得
    • グループID取得のためのBOTが必要
  4. 定型文を送信するBOTの作成
  5. スケジューリングの設定

LINE Messaging APIについて

メッセージはLINE側のサーバー(API)に指定された形式で送る必要がある. 複数人とのグループトークに「Hello World!」というメッセージを送りたい場合, 次のようなリクエストになる.

curl -v -X POST https://api.line.me/v2/bot/message/push \
-H 'Content-Type: application/json' \
-H 'Authorization: Bearer {CHANNEL_ACCESS_TOKEN}' \
-H 'X-Line-Retry-Key: {UUID}' \
-d '{
    "to": "{GROUP_ID}",
    "messages":[
        {
            "type":"text",
            "text":"Hello World!"
        }
    ]
}'
  • UUID : 開発者自身が一意のリトライキーを生成する必要がある[1].
  • CHANNEL_ACCESS_TOKEN : 次節で取得する.
  • GROUP_ID: 次々節で取得する.
    • USER_ID: 個人宛の場合はユーザIDになる.

チャンネルアクセストークンの取得

その際に認証として使われる,チャンネルアクセストークンを取得する.

  • LINE Official Account Managerにログインする.
    • 利用したいアカウントを選択
    • 「設定」→「Messaging API」を選択
    • 「Messaging APIを利用する」をクリック
    • プロバイダーを作成する
      • LINE Official Account Manager にログインするときに使っているアカウントで、LINE Developersコンソールにログインしたことがない場合は、操作の途中で、開発者情報を登録する画面が表示されます。名前とメールアドレスを入力して開発者アカウントを作成します。[2]
      • プラポリや規約は必要なければ空欄でよい
  • LINE Developersにログインする.
    • コンソールに移動する.
    • 対象のプロバイダーとチャネル（Messaging APIを利用するボット）を選択.
    • 「Messaging API」タブに移動
    • 「チャネルアクセストークン（長期）」がある
      • 必要に応じて「発行」ボタンをクリックしてアクセストークンを生成し、その値をコピーする.

グループID(ユーザID)の取得

グループIDの取得するにはサーバが(一時的に)必要になる. Webhookという仕組みを使っているとのこと. 専用のサーバを一から用意するのは大変なので, GAS(Google Apps Script)で行う.

GAS スクリプトの作成

  • Google Driveを開き, 「新規」→「その他」→「Google Apps Script」を選択
  • 次のコードを入力
    • 取得したグループID（ユーザID）を返信する方法として,次の2種類を用意
      1. LINEへIDを返す（返信メッセージを送信）sendReplyToLine
      2. スプレッドシートにIDと現在時刻を保存する saveIdToSpreadsheet
// LINEのBearer認証用アクセストークン。実際のトークンに置き換えてください。
// Access token for LINE Bearer Authorization. Replace with your actual token.
const LINE_CHANNEL_ACCESS_TOKEN = "XXXXXXXXXXXXXXXXXXXXXXX";

// スプレッドシートのID。実際のIDに置き換えてください。
// Spreadsheet ID. Replace with your actual ID.
const SPREADSHEET_ID = "XXXXXXXXXXXXXXXXXXXXXXX";

/**
 * POSTリクエストを処理する関数。
 * Handles POST requests from LINE.
 *
 * @param {Object} eventData - POSTデータを含むイベントオブジェクト / Event object containing the POST data.
 */
function doPost(eventData) {
  // POSTデータを解析し、イベント配列の最初のイベントを取得する
  // Parse the POST data and extract the first event from the array.
  const jsonData = JSON.parse(eventData.postData.contents);
  const lineEvent = jsonData.events[0];

  // 返信メッセージを送信するためのreplyTokenを抽出する
  // Extract the reply token used to send a response message.
  const replyToken = lineEvent.replyToken;

  // ソースの種類（ユーザーまたはグループ）を判定し、対応するIDを設定する
  // Determine the source type (user or group) and assign the corresponding id.
  const sourceType = lineEvent.source.type;
  let sourceId;
  if (sourceType === 'user') {
    sourceId = lineEvent.source.userId;
  } else if (sourceType === 'group') {
    sourceId = lineEvent.source.groupId;
  } else {
    throw new Error("`lineEvent.source.type` is not `user` or `group`.");
  }

  // 好みの方(あるいはどちらも)を選ぶ: 以下の2つの関数のどちらか、または両方を呼び出すことが可能です。
  // Choose either (or both) of the following functions as desired.

  // LINEへIDを返す（返信メッセージを送信）
  // Return the id back to LINE by sending a reply message.
  sendReplyToLine(replyToken, sourceId, sourceType);

  // スプレッドシートにIDと現在時刻を保存する
  // Save the id and current timestamp to a spreadsheet.
  saveIdToSpreadsheet(sourceId);
}

/**
 * スプレッドシートにIDとタイムスタンプを保存する関数。
 * Save the id and a timestamp to a spreadsheet.
 *
 * @param {string} sourceId - 保存するソースID / The source id to save.
 */
function saveIdToSpreadsheet(sourceId) {
  // 指定されたIDのスプレッドシートを開く
  // Open the spreadsheet by its ID.
  const spreadsheet = SpreadsheetApp.openById(SPREADSHEET_ID);
  
  // 「シート1」を取得する
  // Get the sheet named "シート1".
  const sheet = spreadsheet.getSheetByName("シート1");
  
  // 最後に値が入力されている行番号を取得し、次の行に値を書き込む
  // Get the last row with data and write the id in the next row.
  const lastRow = sheet.getLastRow();
  // IDを1列目に保存
  // Save the source id in the first column.
  sheet.getRange(lastRow + 1, 1).setValue(sourceId);
  // 現在のタイムスタンプ（ミリ秒）を2列目に保存
  // Save the current timestamp (in milliseconds) in the second column.
  sheet.getRange(lastRow + 1, 2).setValue(Date.now());
}

/**
 * LINEに返信メッセージを送信する関数。
 * Send a reply message to LINE.
 *
 * @param {string} replyToken - 返信用トークン / Token to reply to the message.
 * @param {string} sourceId - 送信するソースID / The source id to include in the reply.
 * @param {string} sourceType - ソースの種類（user, group, etc.） / The type of the source.
 */
function sendReplyToLine(replyToken, sourceId, sourceType) {
  // LINE APIのエンドポイントURL
  // LINE API endpoint to reply to messages.
  const url = 'https://api.line.me/v2/bot/message/reply';

  // 返信メッセージのペイロードを作成する
  // Build the payload for the reply message.
  const payload = {
    replyToken: replyToken,
    messages: [
      {
        type: 'text',
        text: `${sourceType}_id = ${sourceId}`  // メッセージにソースの種類とIDを表示 / Create a message showing the type and id.
      }
    ]
  };

  // HTTPリクエストのオプションを設定する（メソッド、ヘッダー、ペイロードなど）
  // Setup the HTTP request options, including method, headers, and payload.
  const options = {
    method: 'post',
    headers: {
      'Content-Type': 'application/json; charset=UTF-8',
      'Authorization': 'Bearer ' + LINE_CHANNEL_ACCESS_TOKEN,
    },
    payload: JSON.stringify(payload)
  };

  // UrlFetchAppを使用してLINEに返信メッセージを送信する
  // Send the reply message to LINE using UrlFetchApp.
  UrlFetchApp.fetch(url, options);
}
  • 右上「デプロイ」→「新しいデプロイ」
    • 種類は「ウェブアプリ」
      • 「実行者」は「自分」
      • 「アクセスできるユーザ」は「全員」
      • 説明文などは任意
    • 諸々の確認を承認する
    • デプロイができたら, ウェブアプリのURLをコピーする
  • LINE Developers コンソールから再び, 使いたいチャネルを選択
    • 「Messaging API設定」の「Webhook URL」に先ほどコピーしたリンクを貼る
    • Webhookの利用をオンにする
  • LINEのグループにBOTを招待する（またはメッセージを送る）ことでIDを入手できる.

定型文を送信するBOTの作成

GAS スクリプトの作成(再び)

  • Google Driveを開き, 「新規」→「その他」→「Google Apps Script」を選択
  • 次のjavascriptを貼る
// LINEのBearer認証用アクセストークン。実際のトークンに置き換えてください。
// Access token for LINE Bearer Authorization. Replace with your actual token.
const LINE_CHANNEL_ACCESS_TOKEN = "XXXXXXXXXXXXXXXXXXXXXXX";

// 送信相手のグループID。実際のIDに置き換えてください。
// Replace with receiver actual ID.
const GROUP_ID = "XXXXXXXXXXXXXXXXXXXXXXX";

function main() {
  const message = "Hello, World!";
  pushTextV2MessageToLine(GROUP_ID, message, null, Utilities.getUuid());
}

/**
 * LINEにプッシュメッセージ（textV2）を送信する関数。
 * Send a push message (textV2) to LINE.
 *
 * @param {string} targetId - 送信先のグループIDまたはユーザーID / The target group or user ID.
 * @param {string} messageText - 送信するメッセージのテキスト / The text of the message to send.
 * @param {Object} substitution - プレースホルダーの置換内容（空の場合は空オブジェクトかnull） / The substitution object for placeholders (empty if none).
 * @param {string} retryKey - X-Line-Retry-Key用のUUID / The UUID for the X-Line-Retry-Key header.
 */
function pushTextV2MessageToLine(targetId, messageText, substitution, retryKey) {
  // LINE APIのプッシュメッセージ用エンドポイントURL
  // LINE API endpoint for push messages.
  const url = 'https://api.line.me/v2/bot/message/push';

  // 送信するペイロードの基本形を作成する
  // Build the base payload for the push message.
  const messagePayload = {
    type: "textV2",
    text: messageText
  };

  // substitutionが有効なオブジェクトの場合のみペイロードに追加する
  // Only add substitution if it is a valid, non-empty object.
  if (substitution && Object.keys(substitution).length > 0) {
    messagePayload.substitution = substitution;
  }

  const payload = {
    to: targetId,
    messages: [messagePayload]
  };

  // HTTPリクエストのオプションを設定する（メソッド、ヘッダー、ペイロードなど）
  // Setup the HTTP request options, including method, headers, and payload.
  const options = {
    method: 'post',
    headers: {
      'Content-Type': 'application/json',
      'Authorization': 'Bearer ' + LINE_CHANNEL_ACCESS_TOKEN,
      'X-Line-Retry-Key': retryKey
    },
    payload: JSON.stringify(payload)
  };

  // UrlFetchAppを使用してLINEにプッシュメッセージを送信する
  // Send the push message to LINE using UrlFetchApp.
  UrlFetchApp.fetch(url, options);
}
  • main関数を実行することで, "Hello World!"を受け取れるはず.
  • トリガーを設定すれば定時実行できる.

参考文献

  • [1] LINE Messaging API reference (LINE Developers) - テキストメッセージ(v2) link
  • [2] Messaging APIを始めよう(LINE Developers) link

正十二面体の外接球半径

数学

この記事は旧ブログからの移植です.

(各ページ右上の「内接球半径」は誤りで、「外接球半径」が正しいです)

ここから検索用: 上図は一辺の長さが1である正十二面体である. この正十二面体の外接球の半径を求めたい. (1) $\cos 36\Deg$, ACの長さをそれぞれ求めよ. (2) $\bekutoru{AB}=\beku{b}, \bekutoru{AE}=\beku{e}, \bekutoru{AF}=\beku{f}$とする. $\beku{b}\cdot\beku{e}$を求めよ. (3) $\bekutoru{AC}=\beku{u}, \bekutoru{AG}=\beku{v}, \bekutoru{AN}=\beku{w}$とする. $\beku{u}\cdot\beku{v}$を求めよ. (4) 六面体ACLN-GISPが立方体であることを示せ. (5) 一辺の長さが1であるような正十二面体の外接球の半径を求めよ. (1) $\theta = 36 \Deg$とする. \textrm{AC}&=2\cdot\textrm{AB}\cos 36\Deg
= 2\cos\theta\ \textrm{CD}&=2\cdot\textrm{AC}\cos 72\Deg
= 4\cos\theta\cos 2\theta $\textrm{CD}=1$より 4\cos\theta\cos 2\theta &= 1\ 4\cos\theta \left( 2\cos2\theta - 1 \right) -1 &= 0 \tyuu{2倍角の公式}\ 8\cos3\theta -4\cos\theta -1 &=0\ (2\cos\theta + 1)(4 \cos2\theta - 2 \cos\theta - 1) &= 0 \tyuu{因数定理を用いると良い.}\ \therefore \cos\theta &= -\dfrac{1}{2}, \dfrac{1\pm\sqrt{5}}{4} \intertext{$\theta=36\Deg$より, $\cos\theta >0$だから} \therefore \cos \theta &= \dfrac{1 + \sqrt{5}}{4} したがって, $\textrm{AC} = 2\cos\theta = \dfrac{1+\sqrt{5}}{2}$ (2) 内積の定義より \beku{b}\cdot\beku{e} &= |\bekutoru{AB}||\bekutoru{AE}|\cos 108\Deg ここで3倍角の公式を用いると \cos 108 \Deg = \cos 3\theta &= 4\cos3\theta -3\cos\theta\ &= \cos\theta(4\cos2\theta -3\cos\theta)\ &= \dfrac{1 + \sqrt{5}}{4}\cdot \left{ 4\cdot\left( \dfrac{1 + \sqrt{5}}{4} \right)2 - 3 \right} \ &= \dfrac{1 + \sqrt{5}}{4}\cdot\dfrac{- 6 + 2\sqrt{5}}{4} &= \dfrac{1-\sqrt{5}}{4} したがって, \beku{b}\cdot\beku{e} = |\bekutoru{AB}||\bekutoru{AE}|\cos 108\Deg = 1\cdot 1\cdot\dfrac{1-\sqrt{5}}{4} =\dfrac{1-\sqrt{5}}{4} (2)と同様にして \beku{b}\cdot\beku{e} = \beku{e}\cdot\beku{f} = \beku{f}\cdot\beku{b} = \dfrac{1-\sqrt{5}}{4} となることがわかる. (3) $\beku{u}, \beku{v}, \beku{w}$を $\beku{b}, \beku{e}, \beku{f}$で表す. \beku{u}=\bekutoru{AC} &=\bekutoru{AE} + \bekutoru{EC}\ &=\bekutoru{AE} + \dfrac{1 + \sqrt{5}}{2}\bekutoru{AB} \tyuu{$\textrm{CE}\heikou\textrm{AB}$および,\ CEの長さが$\dfrac{1+\sqrt{5}}{2}$より.}\ &=\beku{e} + \dfrac{1 + \sqrt{5}}{2}\beku{b} 同様にして, \beku{u}= \beku{e} + \dfrac{1 + \sqrt{5}}{2}\beku{b}\ \beku{v}= \beku{b} + \dfrac{1 + \sqrt{5}}{2}\beku{f}\ \beku{w}= \beku{f} + \dfrac{1 + \sqrt{5}}{2}\beku{e} \end{empheq} これを用いると \beku{u} \cdot \beku{v} &= \left( \beku{e} + \dfrac{1 + \sqrt{5}}{2}\beku{b} \right) \cdot \left( \beku{b} + \dfrac{1 + \sqrt{5}}{2}\beku{f} \right)\ &= \dfrac{1+\sqrt{5}}{2}|\beku{b}|^2 + \beku{b}\cdot\beku{e} + \dfrac{1+\sqrt{5}}{2}\beku{e}\cdot\beku{f} + \left( \dfrac{1+\sqrt{5}}{2} \right)2 \beku{b}\cdot\beku{f}\ &= \dfrac{1+\sqrt{5}}{2} + \dfrac{1-\sqrt{5}}{4} + \dfrac{1+\sqrt{5}}{2}\cdot\dfrac{1-\sqrt{5}}{4} + \left( \dfrac{1+\sqrt{5}}{2} \right)2\cdot\dfrac{1-\sqrt{5}}{4}\ &= 0 同様にして \beku{u} \cdot \beku{v} = \beku{v} \cdot \beku{w} = \beku{w} \cdot \beku{u} = 0 (4) (3)より, $\textrm{AC}\perp\textrm{AG}, \textrm{AG}\perp\textrm{AN}, \textrm{AN}\perp\textrm{AC}$である. 対称性から,交わる辺はすべて直交することがわかるから, ACLN-GISPは直方体となる. またすべての辺の長さは等しい. したがってACLN-GISPは立方体. (5) 正十二面体の対角線のなかで, 最長のものが外接球の直径$2R$になるが,これはCP間の距離に等しい. (4)より,これはACLN-GISPの対角線の長さに等しく,その長さは 2R &=\sqrt{|\beku{u}|^2 + |\beku{v}|^2 + |\beku{w}|^2}\ &= \sqrt{3}|\beku{u}|\ &= \sqrt{3}\cdot\dfrac{1+\sqrt{5}}{2}\ &= \dfrac{\sqrt{3} + \sqrt{15}}{2}\ \therefore R &= \dfrac{\sqrt{3} + \sqrt{15}}{4}

iPhone標準カレンダーに、共有されたGoogleカレンダーを表示する方法

技術系の何か

背景

Google カレンダーを iPhone (Apple) の標準カレンダーに同期する方法については多くの解説がある.

しかし, 「Google カレンダーの共有カレンダー」（以下, 単に共有カレンダー）を iPhone の標準カレンダーへ同期する方法は手順が分かりづらいにもかかわらず, 十分に共有されていない.

他人・別アカウントの Google カレンダーを iPhone カレンダーに同期したい場合の具体的な解決策を示す.

結論

  1. https://calendar.google.com/calendar/syncselectにアクセス
  2. iPhone カレンダーへ登録したい共有カレンダーにチェック
  3. 最後に「保存」を押す

チェックを入れて「保存」を押すだけ

最後に二言

いつの時代のUIやねん.

Googleカレンダーの設定ページにちゃんと入れておいてくれ.

CSVファイルをGoogleカレンダーへインポートする

技術系の何か

目次

CSVファイルの作成

項目 要件 表示
Subject 必須 予定のタイトル
Start Date 必須(yyyy/mm/dd) 開始日
Start Time 任意(hh:mm) 開始時刻
End Date 任意(yyyy/mm/dd) 終了日
End Time 任意(hh:mm) 終了時刻
All Day Event 任意(True/False) 終日の予定か
Descrirption 任意 詳細欄
Location 任意 場所
Private 任意(True/False) 限定公開か

上記の形式に則ったCSVファイルとして保存する.

ヘッダコピー用

Subject Start Date  Start Time  End Date    End Time    All Day Event   Descrirption    Location    Private

csv例

余談

解説記事によっては, Reminder On/Off, Reminder Date などのヘッダが記載されていることがある. これはおそらく古いバージョンのもので, 現在は使えないヘッダのようである.

公式の情報はここにある.

csvヘッダの説明(https://support.google.com/calendar/answer/37118?hl=ja&visit_id=638782121743444702-2902216615&rd=1#zippy=%2Ccsv-%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB%E3%81%AE%E4%BD%9C%E6%88%90%E3%81%A8%E7%B7%A8%E9%9B%86 より引用)

Google カレンダーにインポート

Google カレンダーの設定を開く(歯車マーク→設定).

Google カレンダーの設定

左のメニューから、「インポート・エクスポート」を選ぶ. 「パソコンからファイルを選択」から、先程保存したCSVを選び、追加したいカレンダーを指定して,インポートをクリック.

インポート画面

おまけ

競技かるたの大会名から、適切な省略形を手に入れるための正規変換を考える.

不要な情報としては

"第.*回|全国|競技かるた|小倉百人一首|大会|\(.*\)|（.*）|※|\s"

なので、例えばExcelで変換する場合には REGEXREPLACE(A1,"第.*回|全国|競技かるた|小倉百人一首|大会|\(.*\)|（.*）|※|\s","") を用いれば良い.

文書から予定をGoogleカレンダーに追加する【ChatGPT】2025/03

技術系の何か

やりたいこと

「大会要項」が書かれた文書(PDFまたはWord形式)をChatGPTに読ませて, ChatGPTに要約させた後, 「申込締切日」と「大会開催日」をGoogleカレンダーに追加する.

完成したものはこれ

具体的なフロー

やり取りはすべてchatGPTとのチャット画面で行う.

  1. ユーザーがPDFまたはドキュメントをアップロード。
  2. 指定フォーマットで文章を作成し、ユーザーへ確認を求める。
  3. ユーザーがOKあるいは修正点を送信。
  4. 「会〆、本〆 *1、 大会当日のスケジュールをGoogleカレンダーに追加するための情報」をユーザーに提示。
  5. ユーザーが確認し、OKを送信。
  6. 「会〆、本〆、大会当日のスケジュール」をGoogleカレンダーに追加（OpenAPI Specificationを用いる）。

目次

必要なもの

  • ChatGPTのmyGPT機能(作成)
    • 記事執筆時点では有料版限定の機能
  • Google Cloud Console

OAuth認証するユーザはGoogle Calendarのユーザと一致しなくても良い. この場合、最後に設定するテストユーザに、OAuth認証するユーザを追加する.

Google Cloud の設定

https://console.cloud.google.com/welcome を開いて、 上部の「プロジェクトの選択」→「新しいプロジェクト」を作成する.

Google Cloudのトップページ

プロジェクト名はわかりやすければ何でも良い.

新しいプロジェクトの作成画面

上部の検索バーから"Google Calendar API"を検索しクリックし、Google Calendar API を「有効にする」をクリック.

検索バー

Google Calendar API

右上「認証情報を作成」.

Google Calendar API の詳細

認証情報を作成する.

  • APIを選択→Google Calendar API
  • アクセスするデータ→ユーザーデータ
  • アプリ名→わかりやすければ何でも(ログイン画面でも出るので分かりやすい名前に)
  • メール→（自分だけが今回のサービス使うなら）使うことはない
  • ロゴ→不要
  • スコープ→Calendar.events （今回は予定の追加権限がほしいため）
  • OAuth クライアントID →ウェブアプリケーション（GPTが使うため）
  • 名前→適当に

これでひとまず作成は完了. 後ほど戻って来る.

myGPTの作成

ここからChatGPT.

myGPTをクリックし「GPTを作成する」を選択、その後左下「新しいアクションを作成する」をクリック.

メニュー

アクションの追加画面に来る. OpenAPI スキーマを入力する必要があるが、書き方がわからなければGPTに聞くと教えてくれる. 一応、例を本記事下部に掲載する. 例を下にGPTに尋ねるとカスタマイズしてくれるだろう.

アクションを追加

GPTとGoogleカレンダーの連携設定

【GPT】OAuth認証の設定

上記の続き, アクションの追加画面上部の「認証」を選択する. 「OAuth」を選択.

OAuth設定画面

この画面を次のように埋める.

Google Cloudに戻り、 「APIとサービス」→「認証情報」→「OAuth2.0 クライアントID」から作ったものを選択. このページ★にはすぐ戻ってくるので、開けたままにする. クライアント IDとクライアントシークレットがそれぞれ表示されるので、コピペする.

APIとサービス→認証情報

【Google Cloud】OAuth認証の設定

ここまで終えたらmyGPTを保存したうえで、再度myGPTの設定を開く. 先程「アクションを追加」を押した場所に、アクションが設定されているはず. その直下にある「コールバックURL」をコピーする.

アクションの下にコールバックURL

開けっ放しにしておいたページ★(「APIとサービス」→「認証情報」→「OAuth2.0 クライアントID」)に戻ってきて、 「承認済みのリダイレクトURI」に先程の「コールバックURL」を貼り付ける.

最後に「APIとサービス」→「OAuth同意画面」→「対象」→「テストユーザー」を追加して、終了. このテストユーザーはカレンダーのユーザと一致しなくても良い.

テストユーザーの追加

あとはGPTのプロンプト

ここまでで連携部分はできたので、あとはGPTのプロンプトを各々で記載すればよい. 今回の作例は本記事下部に.

完成

1- ユーザーがPDFまたはドキュメントをアップロード。

2- 指定フォーマットで文章を作成し、ユーザーへ確認を求める。*2

4- 「会〆、本〆、大会当日のスケジュールをGoogleカレンダーに追加するための情報」をユーザーに提示。

6- 「会〆、本〆、大会当日のスケジュール」をGoogleカレンダーに追加。

OpenAPI スキーマ例

openapi: 3.1.0
info:
  title: 大会スケジュール管理API
  description: "大会の会〆、本〆、大会当日をGoogleカレンダーに登録するAPI"
  version: 1.0.0

servers:
  - url: "https://www.googleapis.com/calendar/v3"

paths:
  /calendars/{calendarId}/events:
    post:
      operationId: createEvent
      summary: "Googleカレンダーに大会情報を追加"
      description: "指定されたカレンダーに大会情報のイベントを登録"
      parameters:
        - name: calendarId
          in: path
          required: true
          schema:
            type: string
          description: "GoogleカレンダーのID（会〆、本〆、大会当日など任意のもの）"
      security:
        - BearerAuth: []
      requestBody:
        required: true
        content:
          application/json:
            schema:
              type: object
              properties:
                summary:
                  type: string
                  description: "イベントのタイトル"
                start:
                  type: object
                  properties:
                    date:
                      type: string
                      format: date
                      example: "2025-03-07"
                end:
                  type: object
                  properties:
                    date:
                      type: string
                      format: date
                      example: "2025-03-07"
                location:
                  type: string
                  nullable: true
                  description: "開催場所（大会当日のみ）"
                description:
                  type: string
                  nullable: true
                  description: "会〆日（大会当日のみ）"
      responses:
        "200":
          description: "イベントが正常に追加された"
          content:
            application/json:
              schema:
                type: object
                properties:
                  id:
                    type: string
                    description: "イベントID"
        "400":
          description: "リクエストが不正"
        "401":
          description: "認証エラー"
        "500":
          description: "サーバーエラー"

components:
  schemas: {}
  securitySchemes:
    BearerAuth:
      type: http
      scheme: bearer
      bearerFormat: JWT

プロンプト例

このGPTは、ユーザーがアップロードしたPDFファイルから情報を抽出し、特に大会やイベントに関連する情報を指定されたフォーマットに従って整形します。

ワークフロー:
①ユーザーがPDFまたはドキュメントをアップロード。
②「昇級対象」かどうかを尋ねる（それ以外の質問をせず、ただ尋ねる）。
③ユーザーがYes/Noを送信。
④「大会情報フォルダのアドレス」を尋ねる（それ以外の質問をせず、ただ尋ねる）。
⑤ユーザーが「大会情報フォルダのアドレス」を送信。
⑥指定フォーマットで文章を作成し、ユーザーへ確認を求める。
⑦ユーザーがOKあるいは修正点を送信。
⑧「会〆、本〆、大会当日のスケジュールをGoogleカレンダーに追加するための情報」をユーザーに提示。
⑨ユーザーが確認し、OKを送信。
⑩「会〆、本〆、大会当日のスケジュール」をGoogleカレンダーに追加（OpenAPI Specificationを用いる）。

【指定されたフォーマット】
(フォーマットはここから)
----------------------------------------
■■[日付][大会名][級名]・[昇級対象か]■■
□□[計算された締切日]会〆□□

📍場所:[場所] [GoogleマップURL]

参加費:[金額]

📅締切日
会〆:[計算された締切日]
本〆:[申込締切日]

参加資格:[資格]

📁大会情報フォルダ:[ユーザーが提供したアドレス]

(フォーマットはここまで)

フォーマットの改行や順序は完全に遵守し、一切の変更を加えないこと。また、各項目の間に適切な改行を入れ、情報が見やすい形式で出力すること。
PDFに記載されている情報の正確性を優先すること。出力は指定フォーマットの結果のみを表示し、余分な説明や情報は含みません。

さらに、大会名は以下の規則で略記します：
・文字列「全国」「かるた」「競技かるた」「百人一首」「大会」および回数名は取り除く。

本〆は申込締切日を指し、大会開催日ではありません。この点を絶対に間違えないよう、最大限の注意を払います。また、会〆は必ず本〆日の直前の火曜日を計算して記載します。「開催日の直前の火曜日」ではなく、「本〆日の直前の火曜日」であることを厳密に確認します。

すべての日付（会〆日、本〆日、大会開催日）は"mm/dd(曜)"形式に統一し、括弧や中括弧は一切使用しません。
URLを出力する際にはリンク文字列のみを出力し、Markdown形式（[title](link)）は使用しません。

情報は各「級」ごとに分類して整理され、指定フォーマットに従って級ごとにまとめられます。級については、アルファベット1字で表現できる場合は、アルファベット1字のみで表現してください。「初心者級」のように表現できない場合は、記載の通り出力します。この指示を厳格に守り、各級の情報を漏れなく正確に分類します。

場所情報にはGoogleマップURLを生成して追記します。

【Googleカレンダー追加時のフォーマット】（※summaryには空白文字を含めない）
- **会〆**
  - `summary` : "〆"+[級すべて]+"|"+[大会名]+[開催日]+[級すべて]
  - `start`, `end` : [会〆日]（終日の予定）
  - `location` : 空欄
  - `description` : [大会情報フォルダのリンク]

- **本〆**
  - `summary` : "⏰"+[大会名]+[開催日]+[級すべて]
  - `start`, `end` : [本〆日の前日]（終日の予定）
  - `location` : 空欄
  - `description` : 空欄

- **大会当日**
  - `summary` : [大会名]+[級すべて]
  - `start`, `end` : [開催日]（終日の予定）
  - `location` : [場所]
  - `description` : "会〆日"+[会〆日]+"\n"+[大会情報フォルダのリンク]

【GoogleカレンダーID】
- 会〆: ***@group.calendar.google.com
- 本〆: ***@group.calendar.google.com
- 大会当日: ***@group.calendar.google.com

参考文献

カスタムGPTs完全ガイド：GoogleカレンダーAPIを実装した秘書GPTの作り方 | AIじゃないよ

*1:締切が2種類あるのは 「サークル内での締切→会〆」 「主催者側の締切→本〆」 がユースケース的に必要だから.本質的ではない.

*2:実は締切日をchatGPTが間違えていたため、修正の依頼を出しています

定位置と確率【競技かるた】

競技かるた

問題

Aさんの定位置表では, 右下段が25枚あります.

定位置表

Aさんは自陣を25枚並べるとき, 右下段が8枚以上あり「多い」と感じることが ”よくある”と思っております。 それは本当に”よくある”ことなのでしょうか？

答え

Aさんが右下段を「多い」と感じる確率を求めると, 24.9 % です。 ざっくり言えば、4試合に1度は右下段を「多い」と感じていますね。

数値を変えてみるとどうなる

↓定位置表 ＼ 自陣25枚中→ 5枚以上 6枚以上 7枚以上 8枚以上 9枚以上
16枚 36.4 17.1 6.2 1.7 0.4
17枚 42.6 21.7 8.7 2.7 0.6
18枚 48.7 26.7 11.7 4.0 1.1
19枚 54.6 32.1 15.1 5.7 1.7
20枚 60.2 37.6 19.1 7.8 2.5
21枚 65.5 43.3 23.5 10.3 3.6
22枚 70.4 48.9 28.3 13.3 5.1
23枚 74.9 54.4 33.3 16.8 6.9
24枚 78.9 59.7 38.5 20.6 9.1
25枚 82.4 64.8 43.8 24.9 11.6

どのように求めたのか

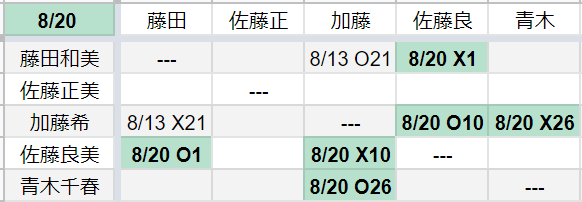
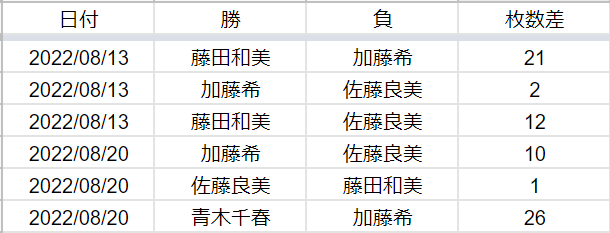
自身の定位置表における右下段の枚数を n 枚とし, 試合で自陣に並べる札25枚のうち, 右下段の枚数を k 枚とします (0\le n \le 100, 0\le k \le 25, k\le n). 25枚中 k 枚が右下段である確率は, 二項係数を用いて

 
\displaystyle 
\frac{ {}_n\mathrm{C}_k \cdot {}_{100-n}\mathrm{C}_{25-k} }{ {}_{100}\mathrm{C}_{25} }

と表せます. したがって, 試合で25枚並べた際に右下段が k 枚以上となる確率 P_{n}(k) は

 
\displaystyle 
P_{n}(k) = 
\sum_{i=k}^{m}
\frac{ {}_n\mathrm{C}_i \cdot {}_{100-n}\mathrm{C}_{25-i} }{ {}_{100}\mathrm{C}_{25} } 
\quad
(m:=\min \{n,25\})

ですね.

上記の表の値は, P_{n}(k) をMathematicaを用いて求め, その値を小数第2位で四捨五入したものです.